3 Task03开始啦！
参照开源文档，观看视频 P5-8：误差和梯度下降（2天），开源文档：https://datawhalechina.github.io/leeml-notes ；视频地址：https://www.bilibili.com/video/BV1Ht411g7Ef

Task 03 误差和梯度下降

误差

  • error due to (1)"bias" and error due to (2)"variance"

  • Estimate the mean of a variable $x$

    • assume the mean of x is $μ$
    • assume the variance of x is $σ^2$
  • 简单的模型bias比较大，var比较小；复杂的模型bias比较小，var比较大。

pic t3-001

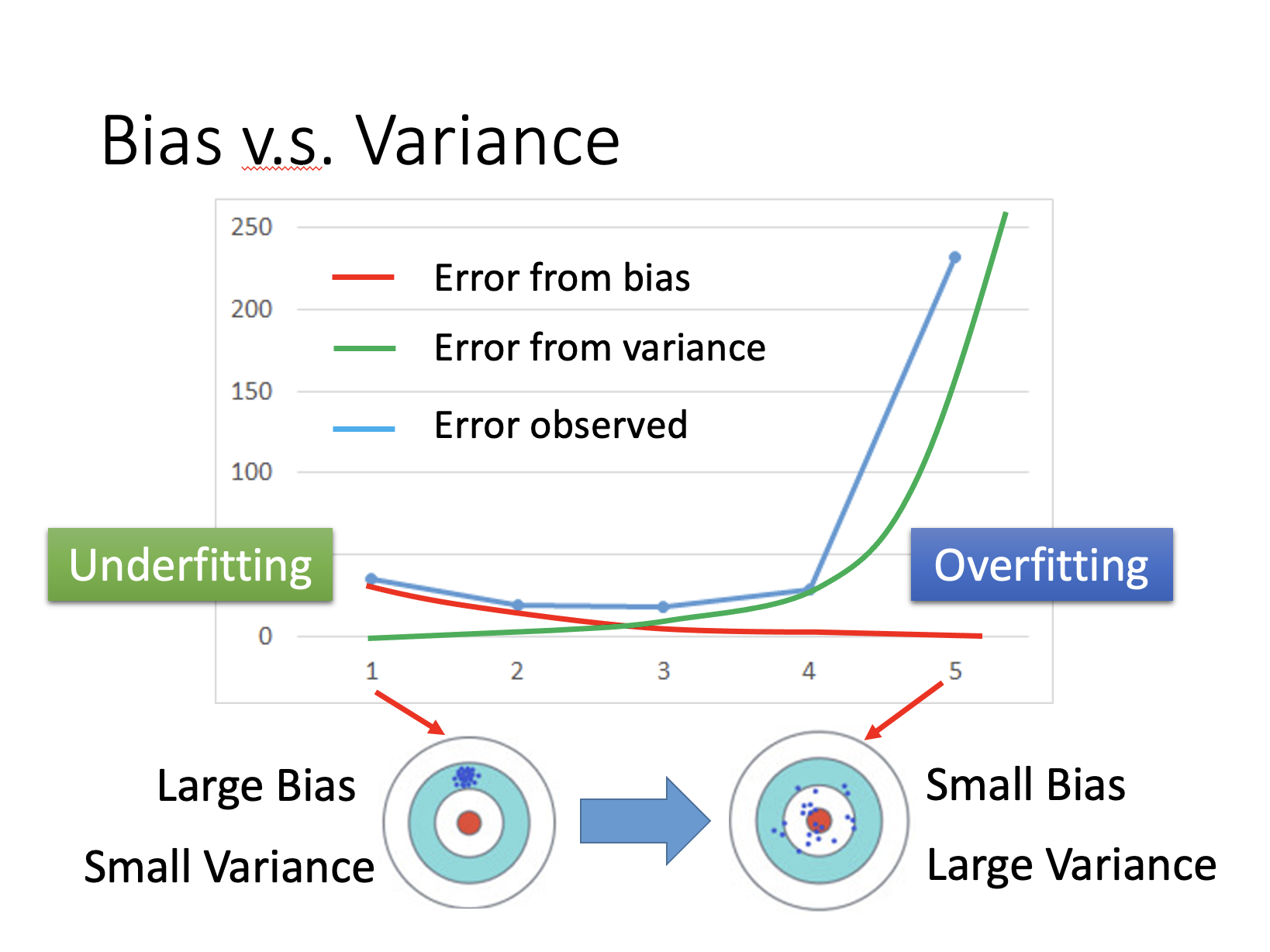
  • Diagnosis:

    • 如果模型没有很好的训练训练集，就是偏差过大，也就是欠拟合 [Underfitting/欠拟合]
    • 如果模型很好的训练训练集，即再训练集上得到很小的错误，但在测试集上得到大的错误，这意味着模型可能是方差比较大，就是过拟合 [Overfitting/过拟合]
    • 对于欠拟合和过拟合，是用不同的方式来处理的

  • 偏差大-欠拟合, redesign your model:

    • 此时应该重新设计模型。因为之前的函数集里面可能根本没有包含f^*f∗。可以：

      • 将更多的函数加进去，比如考虑高度重量，或者HP值等等。
      • 或者考虑更多次幂、更复杂的模型。 如果此时强行再收集更多的data去训练，这是没有什么帮助的，因为设计的函数集本身就不好，再找更多的训练集也不会更好。

  • 方差大-过拟合

    • More data: Very effective, but not always practical
    • Regularization: May increase bias。但是很多时候不一定能做到收集更多的data。可以针对对问题的理解对数据集做调整。比如识别手写数字的时候，偏转角度的数据集不够，那就将正常的数据集左转15度，右转15度，类似这样的处理。

  • 模型选择：

    • 现在在偏差和方差之间就需要一个权衡 想选择的模型，可以平衡偏差和方差产生的错误，使得总错误最小

    • 但是下面这件事最好不要做：

      • 用训练集训练不同的模型，然后在测试集上比较错误，模型3的错误比较小，就认为模型3好。但实际上这只是你手上的测试集，真正完整的测试集并没有。 比如在已有的测试集上错误是0.5，但有条件收集到更多的测试集后通常得到的错误都是大于0.5的。

    • 可以做如下验证来选择好的模型：（将Training Set分为Training set和Validation set）不可以使用Public Testing Set对模型进行调整。

      • 交叉验证
      • N-折交叉验证

梯度下降 (Gradient Descent)

1. Review: 梯度下降法

在回归问题的第三步中，需要解决下面的最优化问题：
$$\theta^∗= \underset{ \theta }{\operatorname{arg\ min}} L(\theta) \tag1$$

  • $L$ :lossfunction（损失函数）

  • $\theta$ :parameters（参数）
    chapter6-1.png
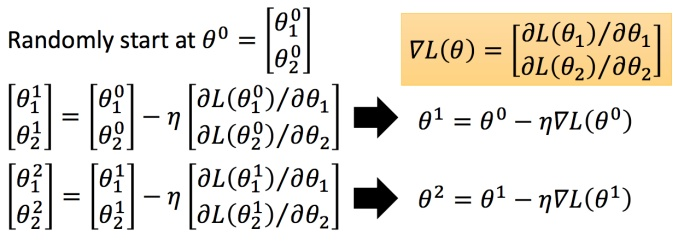
    然后分别计算初始点处，两个参数对 $L$ 的偏微分，然后 $\theta^0$ 减掉 $\eta$ 乘上偏微分的值，得到一组新的参数。同理反复进行这样的计算。黄色部分为简洁的写法，$\triangledown L(\theta)$ 即为梯度。

    $\eta$ 叫做Learning rates（学习速率）
    chapter6-2.png
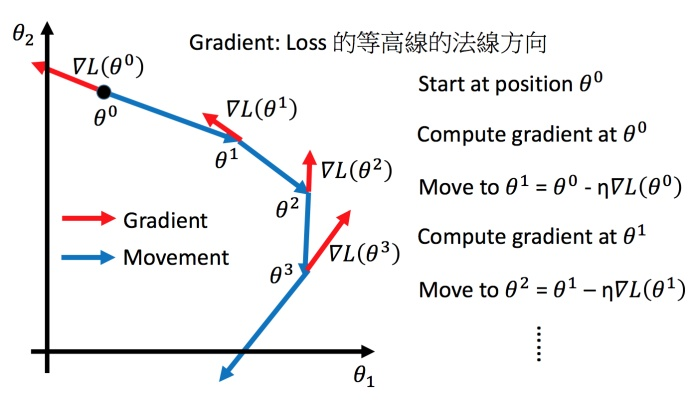
    上图举例将梯度下降法的计算过程进行可视化。

    2. Tip1：调整学习速率

    2.1 小心翼翼地调整学习率

chapter6-3.png

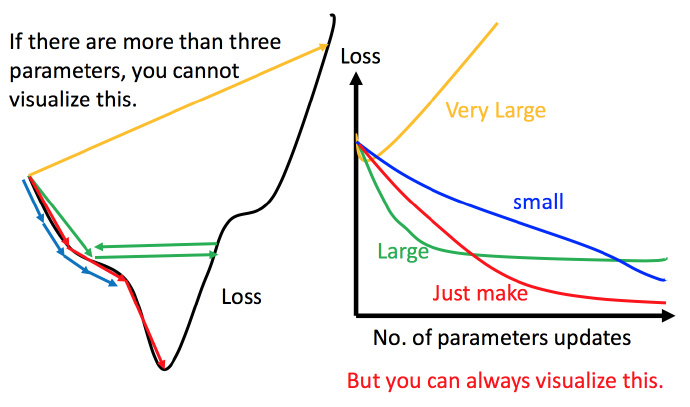
上图左边黑色为损失函数的曲线，假设从左边最高点开始，如果学习率调整的刚刚好，比如红色的线，就能顺利找到最低点。如果学习率调整的太小，比如蓝色的线，就会走的太慢，虽然这种情况给足够多的时间也可以找到最低点，实际情况可能会等不及出结果。如果 学习率调整的有点大，比如绿色的线，就会在上面震荡，走不下去，永远无法到达最低点。还有可能非常大，比如黄色的线，直接就飞出去了，更新参数的时候只会发现损失函数越更新越大。

虽然这样的可视化可以很直观观察，但可视化也只是能在参数是一维或者二维的时候进行，更高维的情况已经无法可视化了。

解决方法就是上图右边的方案，将参数改变对损失函数的影响进行可视化。比如学习率太小（蓝色的线），损失函数下降的非常慢；学习率太大（绿色的线），损失函数下降很快，但马上就卡住不下降了；学习率特别大（黄色的线），损失函数就飞出去了；红色的就是差不多刚好，可以得到一个好的结果。

2.2 自适应学习率

举一个简单的思想：随着次数的增加，通过一些因子来减少学习率

  • 通常刚开始，初始点会距离最低点比较远，所以使用大一点的学习率
  • update好几次参数之后呢，比较靠近最低点了，此时减少学习率
  • 比如 $\eta^t =\frac{\eta^t}{\sqrt{t+1}}$，$t$ 是次数。随着次数的增加，$\eta^t$ 减小

学习率不能是一个值通用所有特征，不同的参数需要不同的学习率.

2.3 Adagrad 算法

  • Adagrad：每个参数的学习率都把它除上之前微分的均方根。

  • Adagrad举例：下图是一个参数的更新过程

    • chapter6-4.png
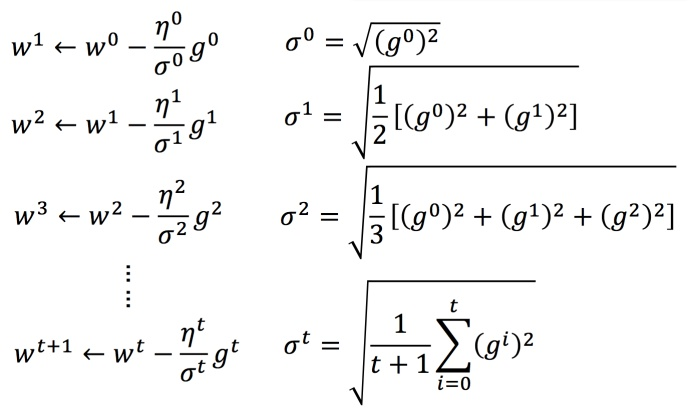
    • 将 Adagrad 的式子进行化简：
    • chapter6-5.png

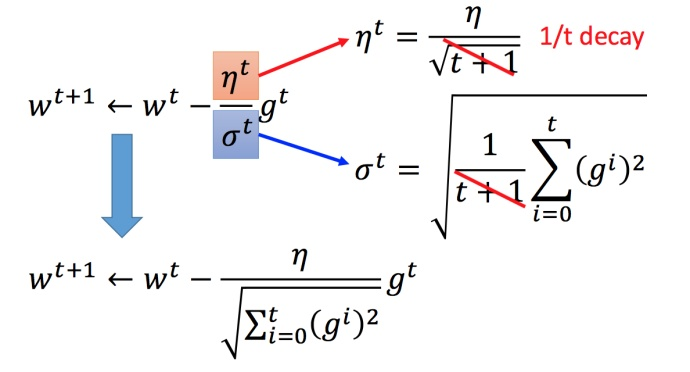
  • 多参数下结论不一定成立

    • 最好的步伐应该是：
    • $$\frac{一次微分}{二次微分}$$
    • 即不止和一次微分成正比，还和二次微分成反比。最好的step应该考虑到二次微分：
    • hapter6-10.png

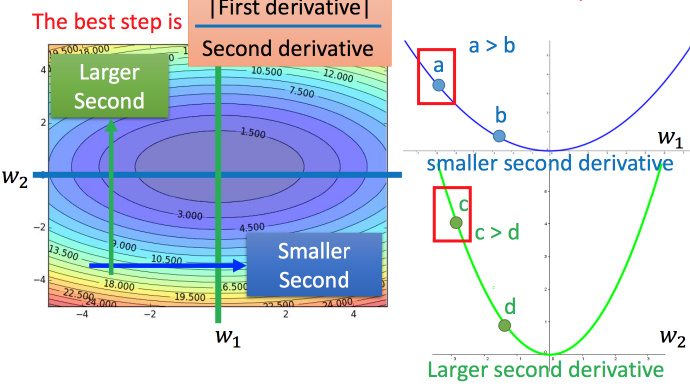
  • Adagrad 进一步的解释

    • 对于 $\sqrt{\sum_{i=0}^t(g^i)^2}$ 就是希望再尽可能不增加过多运算的情况下模拟二次微分。（如果计算二次微分，在实际情况中可能会增加很多的时间消耗）

3 Tip2：随机梯度下降法 (SGD: Stochastic Gradient Descent)

  • 随机梯度下降法更快：损失函数不需要处理训练集所有的数据。
  • 常规梯度下降法走一步要处理到所有二十个例子，但随机算法此时已经走了二十步（每处理一个例子就更新）

4 Tip3：特征缩放

比如有个函数：
$$y=b+w_1x_1+w_2x_2 \tag{12}$$
两个输入的分布的范围很不一样，建议把他们的范围缩放，使得不同输入的范围是一样的。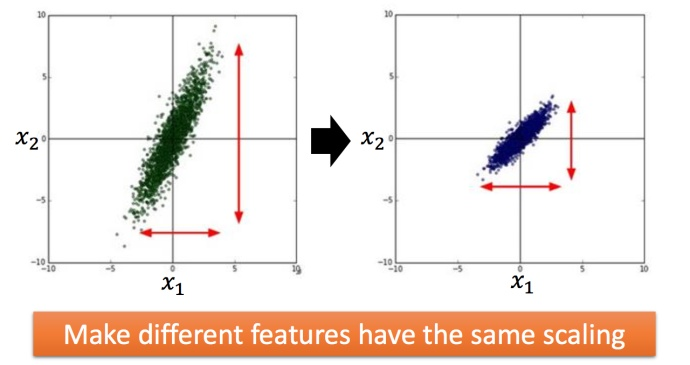
res/chapter6-13.png

4.1 怎么做缩放？

方法非常多，这里举例一种常见的做法：

chapter6-15.png

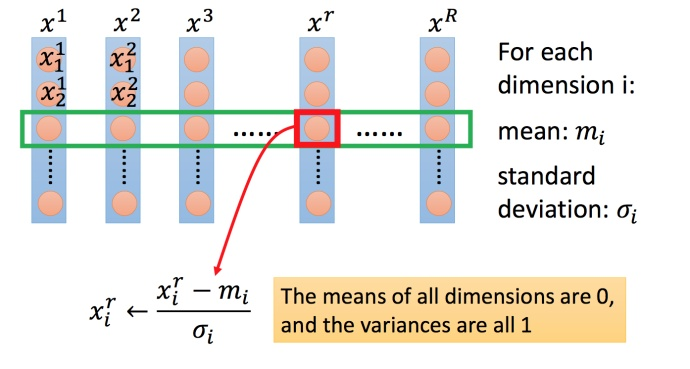
  • 上图每一列都是一个例子，里面都有一组特征。
  • 对每一个维度 $i$（绿色框）都计算平均数，记做 $m_i$；还要计算标准差，记做 $\sigma _i$。
  • 然后用第 $r$ 个例子中的第 $i$ 个输入，减掉平均数 $m_i$，然后除以标准差 $\sigma _i$，得到的结果是所有的维数都是 $0$，所有的方差都是 $1$

5 梯度下降的理论基础

5.1 问题

当用梯度下降解决问题：

$$\theta^∗= \underset{ \theta }{\operatorname{arg\ min}} L(\theta) \tag1$$

每次更新参数 $\theta$，都得到一个新的 $\theta$，它都使得损失函数更小。即：

$$L(\theta^0) >L(\theta^1)>L(\theta^2)>···\tag{13}$$

上述结论正确吗？

结论是不正确的！Update参数后，Loss是不一定会下降的，例如lr太大的时候

5.2 数学理论

  • 泰勒展开式
  • 利用泰勒展开式简化

5.3 梯度下降的限制

chapter6-23.png

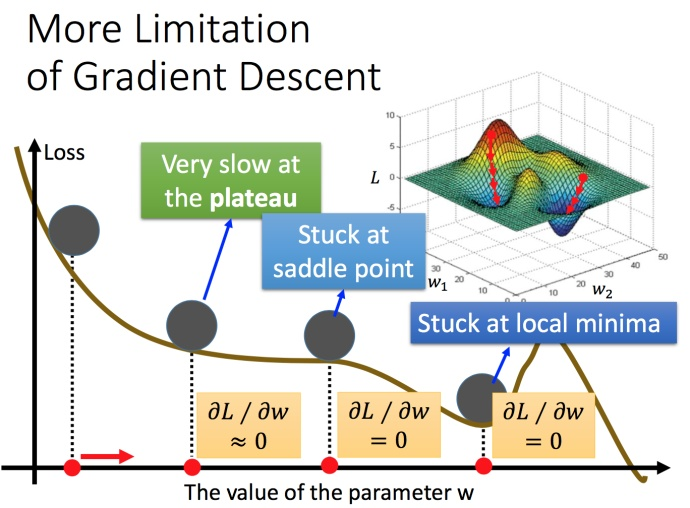
容易陷入局部极值
还有可能卡在不是极值，但微分值是0的地方
还有可能实际中只是当微分值小于某一个数值就停下来了，但这里只是比较平缓，并不是极值点

Reference: